Unifying Random Generation and Shrinking (Property-based Testing Part 4)
This is the fourth post in a series about property-based testing. It describes how to restructure the original QuickCheck API so random generation and shrinking are unified. The first and introductory post in the series is What is it anyway?, followed by The Essentials of Vintage QuickCheck and Shrinking Take One.
\ The complete code for this post can be found on GitHub - in particular example.py and integrated.py.
\
In the last post, we added shrinking to our property-based testing library. This worked well, but we touched on a few not-so-ideal aspects - in particular, that we now need the user to implement and pass in a shrink function to for_all. Besides being an extra burden on the user, it can also lead to some confusing behavior if the generation and shrinking functions are not aligned.
\ Let's look at a contrived example:
\
prop_weird_shrink = for_all(
int_between(-20, -1), shrink_int,
lambda i: i * i < 0
)
\ We're generating strictly negative numbers, and checking that the product of negative numbers is a positive number, but have flipped the greater than sign by mistake.
\ We easily find the bug, but during shrinking a weird thing happens:
\
> test(prop_weird_shrink)
Fail: at test 0 with arguments (-20,).
Shrinking: found smaller arguments (0,)
Shrinking: gave up - smallest arguments found (0,)
\ We report 0 as the smallest element that fails, but 0 wasn't even a possible generated value to begin with! In other words, the shrink candidates don't satisfy the same invariants as the random generator.
\ Can we refactor our API so that it looks and feels like the random generation API but can still shrink? I.e. can our users just write:
\
prop_weird_shrink = for_all(
int_between(-20, -1),
lambda i: i * i < 0
)
\ And get shrinking for free? And of course, while automatically satisfying the same invariants as random generation.
\ The answer turns out to be yes, we can. Let’s see how.
Isn't It Easy?
It's worth explaining briefly why we can't just pack up the interfaces for random generation and shrinking, implement the primitive functions on them and call it a day:
\
class Arbitrary(Generic[Value]):
def generate(self) -> Value:
...
def shrink(self, value: Value) -> Iterable[Value]:
...
\
This is pretty straightforward to implement for int_between for example - we already have random generation and we can pretty easily tweak shrink_int to take low, high arguments and make sure the smaller candidates lie in that range. The real problem occurs when we try to implement map for shrink. We need to support map because we wanted the same API for random+shrink as for random, and random supports map.
\ We'd like to have a function with this signature:
\
def shrink_map(f: Callable[[T],U], s: Shrink[T]) -> Shrink[U]:
def shrinker(value: U) -> Iterable[U]:
...
return shrinker
\
And remember that Shrink[T] just means a function that takes a T and returns an Iterable[T] of smaller values. So the inner shrinker function is the result of shrink_map. Now how to implement it? We could apply f to each candidate generated by the input shrinker s:
\
def shrink_map(f: Callable[[T],U], s: Shrink[T]) -> Shrink[U]:
def shrinker(value: U) -> Iterable[U]:
for candidate in s(...):
yield f(candidate)
return shrinker
\
That would definitely give us a bunch of U candidate values. But the problem is s needs some value T to produce its candidates, and we don't have it! We only have a value U. To drive this point home, here's an example with concrete types - say I want to turn shrink_int into shrink_char - there is, after all, a map of ASCII code integers to characters.
\
Easy, you say, just convert the character to its ASCII code integer using ord, and back to its character using chr:
\
def make_shrink_char(shrink_int: Shrink[int]) -> Shrink[str]:
def shrinker(value: str) -> Iterable[str]:
for candidate in shrink_int(ord(value)):
yield chr(candidate)
return shrinker
\
But this is not a map - in fact to convert a shrink_int into a shrink_char we need two functions: one to convert integers to characters and one to convert characters to integers. With our random map we only have one function to convert one way, and we could do this because generate just has a value it outputs, while shrink needs a value as both input and output.
Ok, so that won't fly. However, we have another shrinking related type which does support map.
Trees, Trees, Trees
To encapsulate the shrinking process, we introduced the CandidateTree class, along with a couple of functions:
\
@dataclass(frozen=True)
class CandidateTree(Generic[T]):
value: T
candidates: Iterable[CandidateTree[T]]
def tree_from_shrink(
value: T,
shrink: Shrink[T]) -> CandidateTree[T]:
# implementation omitted
def tree_map(
func: Callable[[T], U],
tree: CandidateTree[T]) -> CandidateTree[U]:
# implementation omitted
\
Hold on a minute - we can turn any Shrink function into a CandidateTree, and we can implement map for CandidateTree. So it's worth checking if we can also implement mapN and bind for CandidateTree, because that's exactly the interface Random supports. If CandidateTree also supports it, then we could pack up Random and CandidateTree and we'd have our integrated API.
\ We'll see that this is indeed possible. To the best of my knowledge, Reid Draper was the first to come up with this, and implemented it in an early version of the Clojure testing library test.check. Seems obvious only in hindsight!
\
Let's start with mapN then - for clarity I'll show map2 here. The version with n arguments doesn't add anything new, it's just more bookkeeping.
\
Let's first think about what it means to map2 CandidateTrees together. Here's what we need to implement:
\
def tree_map2(
f: Callable[[T, U], V],
tree_1: CandidateTree[T],
tree_2: CandidateTree[U],
) -> CandidateTree[V]:
...
\ As usual, it's easier to look at an example. Here's the trees that shrink 1 and 3 respectively side by side.
\
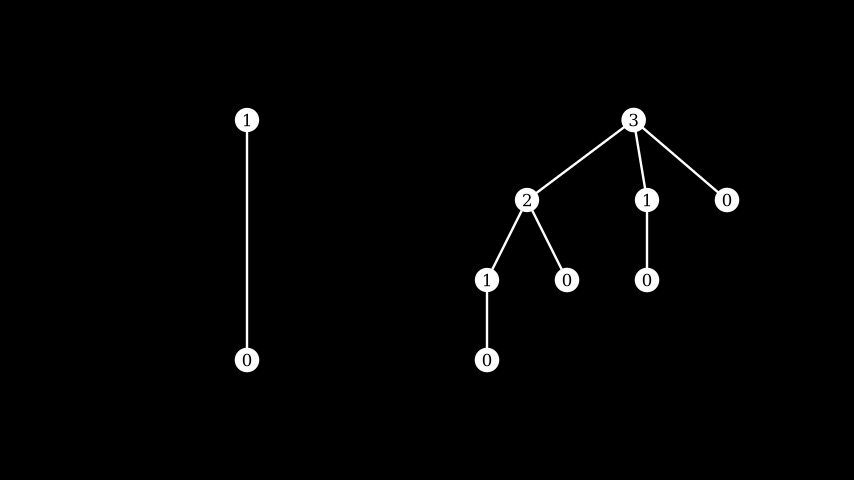 What would it mean to
What would it mean to tree_map2 over those two trees, with f just making a tuple?
\
tree_1 = tree_from_shrink(1, shrink_int(0,10))
tree_2 = tree_from_shrink(3, shrink_int(0,10))
tree_tuples = tree_map2(
lambda x,y: (x,y), tree_1, tree_2)
\
A nice way to think about this is in terms of the resulting tree, which is a tree of tuples of integers. If we know how to shrink each element of a tuple (which we do - those are exactly the two CandidateTree arguments to tree_map2), how would we like to shrink the 2-tuple?
\ How about shrinking the first element first, then the second element - some kind of cross-product of the two trees? The resulting tree looks like:
\
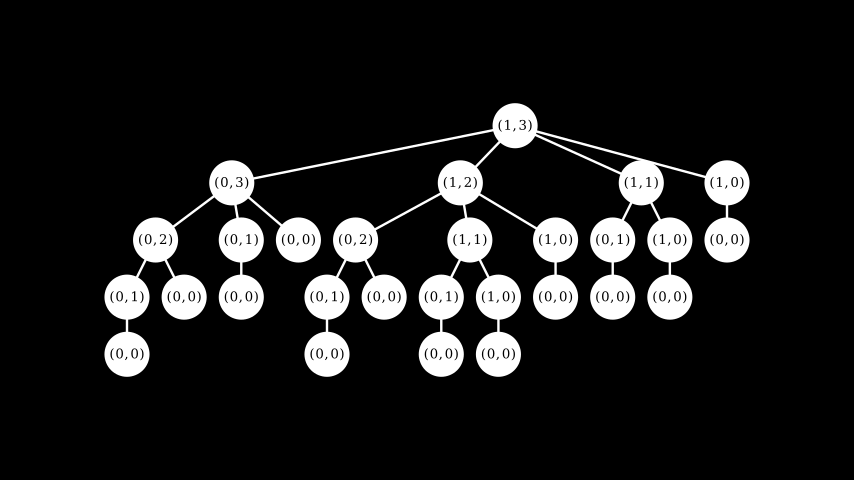
What's going on here? The root of the tree is just (1,3) which corresponds to the roots 1 and 3 of the argument trees. Then the first level below the root of the combined tree, we have four candidates:
\
the first candidate is a combination of the candidate shrink of
tree_1(just 0) with the root oftree_2.the remaining three candidates are a combination of the candidate shrinks of
tree_2with the root oftree_1.\
And this continues recursively as we move down the tree. In code:
\
def tree_map2(
f: Callable[[T, U], V],
tree_1: CandidateTree[T],
tree_2: CandidateTree[U],
) -> CandidateTree[V]:
value = f(tree_1.value, tree_2.value)
candidates_1 = (
tree_map2(f, candidate, tree_2)
for candidate in tree_1.candidates
)
candidates_2 = (
tree_map2(f, tree_1, candidate)
for candidate in tree_2.candidates
)
return CandidateTree(
value = value,
candidates = itertools.chain(
candidates_1,
candidates_2
))
)
\
Sidebar: now that we're doing more interesting things with trees, I've had to change the definition of CandidateTree vs the one in the last post. In particular, the candidates field is now iterated over multiple times - for example in the definition of tree_map2 above. This means we can't just use an iterable anymore, because once that's iterated over, it can't be reset.
\
class CandidateTree(Generic[T]):
def __init__(self, value: T, candidates: Iterable[CandidateTree[T]]) -> None:
self._value = value
(self._candidates,) = itertools.tee(candidates, 1)
@property
def value(self):
return self._value
@property
def candidates(self):
return copy(self._candidates)
\
The implementation details are not important, but what is important for performance is that first, the candidates are evaluated lazily, and second that they are cached. If not, we are either doing too much work, or repeating the same work over and over again.
\
In fact, my original implementation used a simple list in self._candidates but it was extremely slow, to the point where simple tests took several seconds and more involved tests took several minutes.
\
The new definition uses a little trick I picked up somewhere: if you use itertools.tee you can copy the resulting iterable (so it's re-iterated from the start), and itertools.tee also incrementally caches the elements. So in the above code you can read itertools.tee as "return a cached iterator", and copy as "reset the iterator to the start".
\
Let's wrap up this treehugging nonsense by implementing tree_bind. Remember all bind-like functions have a signature like:
\
def tree_bind(
f: Callable[[T], CandidateTree[U]],
tree: CandidateTree[T]
) -> CandidateTree[U]:
...
\
Which allows the caller to inject an arbitrary f that can return an entirely new tree for each element of the input tree tree. This is more powerful than tree_map because map maintains the shape of the tree - no new nodes can be added or removed. tree_map2 also restricts how the shape of the input trees are used - it can only produce a "product" of the input trees.
\
With tree_bind however, the resulting tree can look entirely different, depending on the what f does.
\ I'm just going to chuck the implementation at you, and then discuss it with an example.
def tree_bind(
f: Callable[[T], CandidateTree[U]],
tree: CandidateTree[T]
) -> CandidateTree[U]:
tree_u = f(tree.value)
candidates = (
tree_bind(f, candidate)
for candidate in tree.candidates
)
return CandidateTree(
value = tree_u.value,
candidates = itertools.chain(
candidates,
tree_u.candidates
)
)
\ This practically writes itself - given the arguments and their types, it's pretty hard to come up with anything else (if you aren't trying to be pedantic, like those people who go "yes" when you ask "can you turn on the light?" and then smugly point out they've answered your question while you give them the mental middle finger).
\
The root of the new tree is the result of applying f to the input tree, and taking the root value of the resulting tree. To get the subtrees (the candidates field) we recursively call tree_bind on each of input tree's candidates - giving us a list of trees again. The only decision to make is how to combine candidate and tree_u.candidates: which one should go first? I'm claiming it makes most sense to put candidates first, because that corresponds to the "outer" tree.
\ Let's make sense of that statement, and the implementation, by looking at an example. The example is contrived and not very practical, so I can't spin a nice story around it - it's reminiscent of shrinking a list, where we first want to shrink the length of the list, and then the individual elements.
\
We'll start with a tree that shrinks the integer 3, like we've seen a few times before already. The elements of this tree will determine the length of a string consisting of the letter c. The function letters creates a CandidateTree for a given length, that shrinks length times the letter c to b and then to a. letters is the function we intend to use as the f argument to tree_bind:
\
def letters(length: int):
abc = tree_from_shrink(ord('c'), shrink_int(ord('a'), ord('c')))
abc_repeat = tree_map(lambda o: chr(o) * length, abc)
return abc_repeat
\
Here's the tree that shrinks the integer 3, and the trees returned by letters for length values 1, 2 and 3 respectively:
\
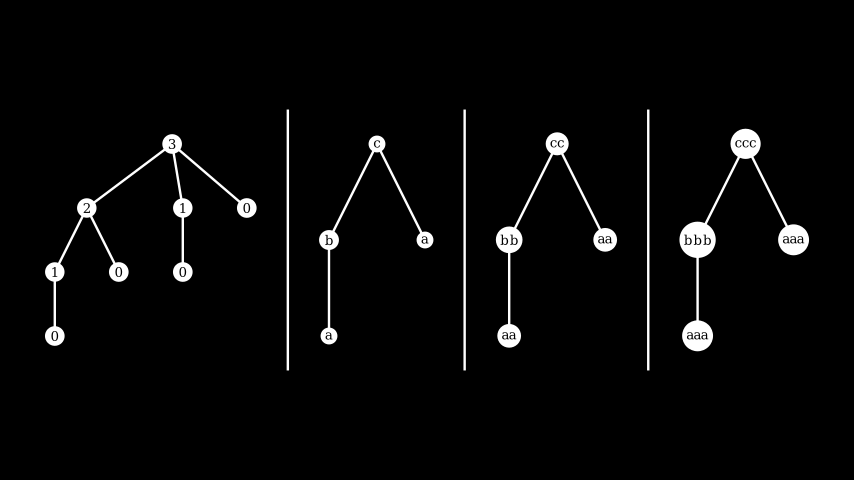
Note while shrinking, letters never changes the length of the string - it only tries to make the letters smaller by moving closer to a.
\
If we now use tree_bind as follows:
tree_list_length = tree_from_shrink(3, shrink_int(0,3))
tree_bound = tree_bind(letters, tree_list_length)
\
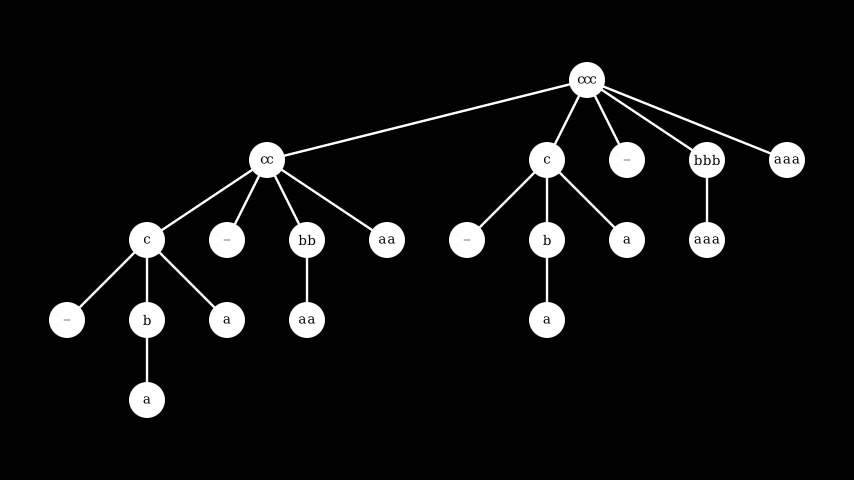
Then tree_bound looks as follows:
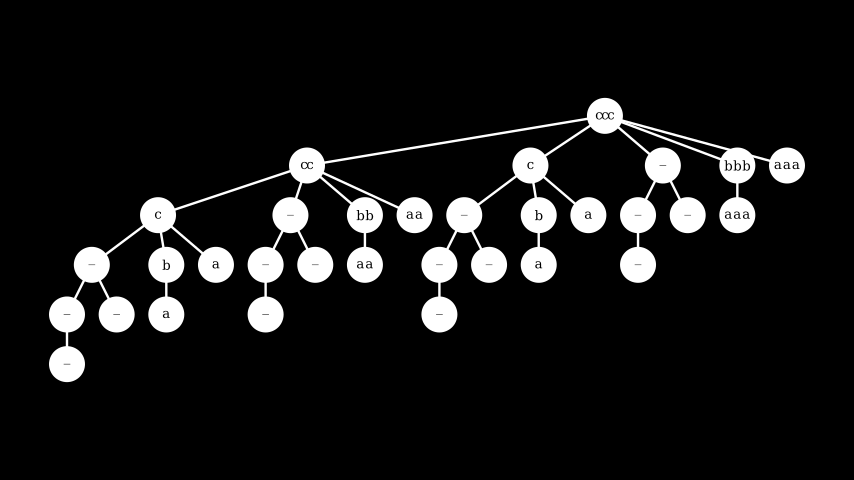
First of all the root node ccc is the result of applying letters to the root of the input tree, so with length = 3. On the first level down, the shrink candidates for ccc are cc, c, - meaning the empty string, bbb and finally aaa. This progression is a direct result of our choice to try the shrinks from the "outer" tree first - the shrink candidates of tree_list_length are 2, 1, and 0 respectively, which results in cc, c and -. The remaining values bbb and aaa are the result of shrinking ccc directly, see the fourth tree in the first image. This continues recursively.
\
One thing you may have noticed in the resulting tree is that several sections are essentially the empty string, repeated a number of times. Where does this come from? If letters is asked to create a tree with length = 0 then it will in fact sill create a tree with a shape that shrinks the value c to b and a, but each candidate letter is repeated 0 times and so becomes the empty string. We can avoid this by making a small change to letters, to return a constant tree without shrinks in case length is 0.
\
def tree_constant(value: T) -> CandidateTree[T]:
return CandidateTree(value, tuple())
def letters(length: int):
if length == 0:
return tree_constant('')
abc = tree_from_shrink(ord('c'), shrink_int(ord('a'), ord('c')))
abc_repeat = tree_map(lambda o: chr(o) * length, abc)
return abc_repeat
\ We then get more reasonably:
\
At first blush this seems like an almost trivial annoyance, but it's not without its consequences. As we'll come back to, this kind of potential inefficiency is part of the cost we'll pay for having an integrated shrinking API, and especially affects usage of bind.
\ Enough about trees - time for a break with a delicious strawberry snack.
Putting Humpty-Dumpty Back Together Again
We are now ready to put everything together so we can run some tests.
\
We'll once again literally reuse our implementation of Random and related functions - but because we're now going to have map, mapN and all the rest of it be the main API, I've prefixed the "old" Random specific functions with random_, for example:
\
def random_constant(value:T) -> Random[T]:
return Random(lambda: value)
\
In a more realistic setup Random and its functions would be in a separate module, as well as CandidateTree and its tree_something functions.
\
With the preliminaries out of the way, the goal of this section is to re-create the Random API, i.e. constant, int_between, map, mapN and bind, but in such a way that the resulting API can both randomly generate values and shrink them, all without requiring the user to somehow keep those two in sync or repeat code.
\ Let's first define the type for this thing which I'll just call a "generator" from now on:
Gen = Random[CandidateTree[T]]
\
We’ve used this idea before to extend our library with shrinking - just like in the last post, instead of randomly generating values T we're generating entire trees of T. But now we do it earlier, which is going to make everything look nicely integrated. Also, thanks to laziness in CandidateTree, we're not actually creating the full tree for each value, as that would be unworkably slow.
\
Let's then start with implementing constant:
\
def constant(value: T) -> Gen[T]:
return random_constant(tree_constant(value))
\
If that isn't a satisfying implementation I don't know what is! We just compose the two constant functions for Random and CandidateTree. Will we be able to keep this up for the rest?
\
def map(func: Callable[[T],U], gen: Gen[T]) -> Gen[U]:
return random_map(lambda tree: tree_map(func, tree), gen)
\
That's a yes for map at least. Let's try int_between:
\
def int_between(low: int, high: int) -> Gen[int]:
return random_map(lambda v: tree_from_shrink(v, shrink_int(low, high)), random_int_between(low, high))
\
A bit hairier, but for reasons. First, shrink_int takes two extra arguments - low and high - which indicate the range in which the shrink candidates are allowed to live. In our last implementation, we always tried to shrink to zero, which was cheating (in my defense, I hid it well…).
\
One of the main advantages of integrating shrinking and random generation, is that it leaves me no way out now. Here's the new implementation of shrink_int - it's similar in complexity to the original:
\
def shrink_int(low: int, high: int) -> Shrink[int]:
target = 0
if low > 0:
target = low
if high < 0:
target = high
def shrinker(value: int) -> Iterable[int]:
if value == target:
return
half = (value - target) // 2
current = value - half
while half != 0 and current != target:
yield current
half = (current - target) // 2
current = current - half
yield target
return shrinker
\
It does a similar thing as before, except it ensures that the candidate shrinks are within the [low,high] interval, and tries to shrink in the direction of target, either low or high whichever is closest to zero.
\
You probably know the drill by now - here is mapN:
\
def mapN(f: Callable[...,T], gens: Iterable[Gen[Any]]) -> Gen[T]:
return random_mapN(lambda trees: tree_mapN(f, trees), gens)
\
Exactly like map! I love it when a plan comes together.
\
Finally, bind. As usual, the black sheep to rule them all (ok, these mixed metaphors are really confusing, sorry)
\
Trying the same approach as map teaches us something:
\
def bind(func:Callable[[T], Gen[U]], gen: Gen[T]) -> Gen[U]:
# DOES NOT WORK
return random_bind(lambda tree: tree_bind(func, tree), gen)
\
Can you see why? Consider the type func returns, and the type tree_bind expects.
\
Spoiler alert: func returns Gen[U], which expanded is Random[CandidateTree[U]].
\
But tree_bind expects func to return just CandidateTree[U]! So how do we get a CandidateTree out of a Random[CandidateTree]? The only option is to generate one:
\
def bind(func:Callable[[T], Gen[U]], gen: Gen[T]) -> Gen[U]:
def inner_bind(value: T) -> CandidateTree[U]:
random_tree = func(value)
return random_tree.generate()
return random_map(lambda tree: tree_bind(inner_bind, tree), gen)
\
This effectively means that if people use bind, the quality of shrinking is potentially not great, because when shrinking the outer value, we randomly re-generate the inner value. The inner value might be why the test failed in the first place though, so we're losing interesting information. The effect of this is that shrinking doesn't work as well as it could. We'll see this problem in an example soon.
Abstraction - You'll Know It When You See It
Now we have all the tools to implement for_all and test again. In fact, beautifully, the implementation of for_all with integrated shrinking is exactly the same as the implementation without shrinking in our very first implementation. Even better, the implementation of test is identical to the one in PBT #3!
\
@dataclass(frozen=True)
class TestResult:
is_success: bool
arguments: tuple[Any,...]
# This is the only change:
# replacing Random with Gen.
Property = Gen[TestResult]
def for_all(gen: Gen[T], property: Callable[[T], Union[Property,bool]]) -> Property:
def property_wrapper(value: T) -> Property:
outcome = property(value)
if isinstance(outcome, bool):
return constant(TestResult(is_success=outcome, arguments=(value,)))
else:
return map(lambda inner_out: replace(inner_out, arguments=(value,) + inner_out.arguments),outcome)
return bind(property_wrapper, gen)
def test(property: Property):
def do_shrink(tree: CandidateTree[TestResult]) -> None:
for smaller in tree.candidates:
if not smaller.value.is_success:
# cool, found a smaller value that still fails - keep shrinking
print(f"Shrinking: found smaller arguments {smaller.value.arguments}")
do_shrink(smaller)
break
else:
print(f"Shrinking: gave up at arguments {tree.value.arguments}")
for test_number in range(100):
result = property.generate()
if not result.value.is_success:
print(f"Fail: at test {test_number} with arguments {result.value.arguments}.")
do_shrink(result)
return
print("Success: 100 tests passed.")
\
We can now write a list[Person] generator identically to how we wrote it without shrinking, and it still shrinks!
\
def list_of_gen(gens: Iterable[Gen[Any]]) -> Gen[list[Any]]:
return mapN(lambda args: list(args), gens)
def list_of_length(l: int, gen: Gen[T]) -> Gen[list[T]]:
gen_of_list = list_of_gen([gen] * l)
return gen_of_list
def list_of(gen: Gen[T]) -> Gen[list[T]]:
length = int_between(0, 10)
return bind(lambda l: list_of_length(l, gen), length)
ages = int_between(0,100)
letters = map(chr, int_between(ord('a'), ord('z')))
simple_names = map("".join, list_of_length(6, letters))
persons = mapN(lambda a: Person(*a), (simple_names, ages))
lists_of_person = list_of(persons)
\ Let's finally see it in action:
\
prop_sort_by_age = for_all(
lists_of_person,
lambda persons_in: is_valid(
persons_in,
sort_by_age(persons_in)))
> test(prop_sort_by_age)
Success: 100 tests passed.
prop_wrong_sort_by_age = for_all(
lists_of_person,
lambda persons_in: is_valid(
persons_in,
wrong_sort_by_age(persons_in)))
> test(prop_wrong_sort_by_age)
Fail: at test 0 with arguments ([Person(name='tnrzar', age=21), Person(name='nwgurq', age=23), Person(name='cbvinc', age=22), Person(name='baouyp', age=40)],).
(127 lines skipped)
Shrinking: gave up at arguments ([Person(name='aaaaaa', age=0), Person(name='aaaaaa', age=0), Person(name='aabaaa', age=0), Person(name='aaaaaa', age=1)],)
\ Great, so it works! Kind of? There's a few things to unpack here.
\ First thing to notice, shrinking takes a lot longer, and the end result is not as great as before. Remember with our not-integrated (disintegrated?) shrinking implementation in the previous post, after about 15 shrinking steps we ended up with:
\
[Person(name='', age=1), Person(name='a', age=0)]
\ There are now 127 shrinks before we end up with a final list of length four, instead of length two.
\
This is a consequence of the fact that the automatic, built-in shrinking is not as good as the purpose-built list shrinker we wrote explicitly before. The automatic shrinking strategy only knows about shrinking in so far as we make the structure explicit - and in this case we chose a length for the list, then generated a random list of persons with that length. So all the automatic shrinker can do is try to make the length smaller, which essentially means chopping off elements at the end of the list.
\
As you may remember the purpose-built shrink_list did a binary chop - trying one half, then the other half of the list. This has three important advantages:
\
shrink_listcreates much better candidates. In the example above the first two elements of the list are not necessary, but the automatic shrinking only tries to remove elements at the end, which makes the test succeed. Automatic shrinking can never remove those first two elements.shrink_listdoes not throw away information about the elements of the list while shrinking the list itself. As we saw above,bindhas no choice but to regenerate the inner value every time it tries to shrink the outer. Concretely, it starts with a list of four persons that fail the test, and the next shrink candidate will be a new randomly generated list with three elements. If that one happens to pass the test, the shrink attempt is not successful. Shrinking becomes partly random whenbindis involved.shrink_listis much faster (in terms of number of shrink candidates) to iterate to a solution, because it is able to split the problem size in half on each iteration.
\
This problem - that bind doesn't shrink well - is a well known problem in the property-based testing world. For example, here's an explanation of it in test.check. As far as I know there isn't a great solution, but the problem can be mitigated well in practice though:
\
The use of
bindin generators is avoided altogether for common types like lists, which typically are built-in to the core PBT library. Usually a bespoke shrink function is implemented for collections and other types, which works in much the same way asshrink_list.Users are discouraged to use
bindif they can usemapormapN.There is sometimes a facility to allow the user to override or extend shrink candidates by implementing a shrink candidate function manually. It's ironic that we have to re-introduce something we just jumped though a bunch of hoops to avoid, but at least it leaves users with an out, in cases where they have to use bind and need good shrink candidates.
\
Final observation is that in the original shrink, Person.name was reduced to the empty string or a single letter, while now the shrunk names are six letter strings. This is actually good! We asked for names to be six letter strings in the first place, recall simple_names = map("".join, list_of_length(6, letters)).
\ And now this invariant is honoured both during generation and shrinking. Before, the shrinker was unaware of this six letter constraint. In this case there wasn't any real bad effect, but in practice you can imagine that any names shorter than 6 letters are validated and rejected, which would put the shrink process on a different code path compared to the original failure, masking the original bug.
Conclusion
Property-based testing libraries with integrated shrinking exist for quite a few languages. The first one to implement it was Clojure's test.check. Since then there have been implementations for Haskell, F#, R and Scala under the Hedgehog umbrella, and probably others I’m not aware of.
\ With the benefit of hindsight, the idea is a relatively straightforward refactor of the original QuickCheck shrinking implementation - I hinted in the last post the answer was already in there, but don't feel bad if you didn't see it. I had been staring at the original QuickCheck code for years and didn't see the opportunity.
\ Despite the appeal, we have discussed a few important trade-offs and issues to be aware of.
\ Besides those, these approaches were all developed in the context of pure or at least pure-by-default functional languages like Haskell and Clojure. As we discussed a few times before, shrinking relies essentially on being able to capture the value-to-shrink as it's being generated, and then repeatedly using that value as the seed to find smaller values. But if the value is not, in fact, a value but some mutable object, and during the test it gets mutated, the shrink candidates won't make any sense, and the shrinking process will get very confused.
\ It stands to reason then, that it took writing a property-based testing library for an imperative language like Python for someone to really think about this and come up with an alternative solution. Hypothesis, a PBT library for Python, manages to achieve an integrated shrinking and random generation API, that works well even for mutable objects, and has a few other advantages as well.
\ Again, in some sense the answer has been with us throughout all these posts, but well hidden. Cryptic much? We'll dive into Hypothesis in the next post, stay tuned.
\ As usual, comment below or discuss on Twitter @kurt2001.
\ Until next time!
\ Also published here.
